FIMMPROP
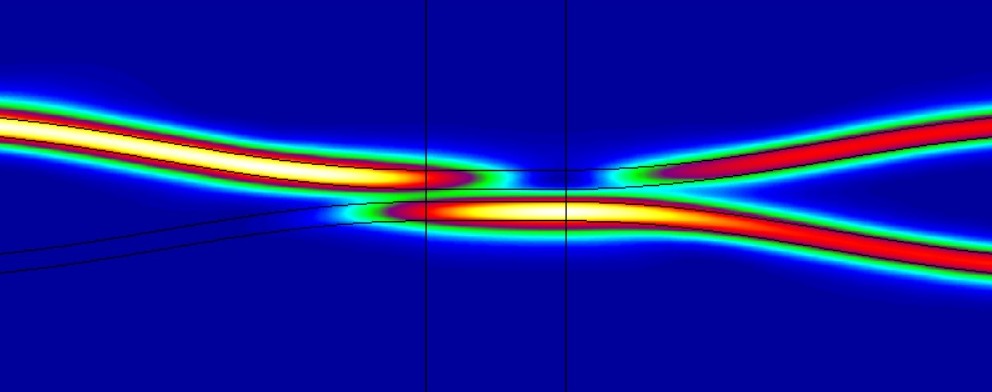
FIMMPROP is a powerful and versatile tool for simulating 2D and 3D optical propagation in waveguides. Through the Eigenmode Expansion Method, it not only provides the simulation result, but also gives a detailed explanation of what's going on within the device, leading to valuable insights that can be used to improve the structures.

features
- An innovative 2D and 3D EigenMode Expansion (EME) tool
- Native 64-bit application (32-bit version is also available)
- Offers a variety of fully vectorial mode solvers, using awide range of robust numerical and semi-analytical methods
- The high index contrast capability makesit suitable for silicon photonics
- Wide and narrow angle
- Rigorous Maxwell Equation solver for semi analytical, fully vectorial 3D propagation
- Mode coupling capability
- Facet coating capability
- Ability to design and simulate MMIs, periodic structures, tapers, and bends quickly and efficiently
- Kallistos for multi-parameter optimization
- Links to ray-racing tools such as FRED
- Scripting capabilities with Python and MATLAB, extensive command-line interface
APPLICATIONS
- Silicon Photonic devices
- Tapers and continuously varying structures
- Optical Fibers
- MMI Couplers
- Gratings and Periodic Devices
- Plasmonic Waveguides
Examples
- Fiber to Chip Silicon Vertical Grating Coupler
-
Inverted Taper for Fiber to Silicon Chip Coupling
-
Optical Ring Resonator Filter
-
An SG-DBR cavity in SOI
-
Planar Y-junction power splitter
-
Directional coupler with S-bends
-
Optimize Taper Designs (with Kallistos)
-
Create optimal S-Bends (with Kallistos)
-
Lensed Fiber for Chip Coupling
-
Tapered Fiber Filter
-
Tapered Metal-coated SNOM Fiber Probe
- Fiber-to-Chip End Coupling
-
Fiber Bragg Gratings
-
Multicore Photonic-Crystal Fiber 1x4 Power Splitter
-
OAM modes and vortex beams
-
1x4 SOI MMI Coupler - Optimisation with Kallistos
-
1x8 AlGaAs MMI Coupler
-
1x2 SOI MMI Wavelength Demultiplexer
-
Wide Bandwidth Grating-Assisted Directional Coupler
-
Grating-Assisted Spot-Size Converter
-
Optical Modes of a Laser Cavity (VCSEL, DFB)
-
Anti-Reflection coating for silicon waveguide facet
Request a Demo

Photon Design Module map
This module map provides a visual overview of the Photon Design software suite, showing how the different tools connect to support your integrated photonics simulations. It starts with the core FIMMPROP module and includes key combinations such as Harold and PICWave. The size of each module indicates its relative role in the design process, while the black lines represent the data flow between components. Together, these tools form a cohesive environment for designing and optimizing photonic devices.
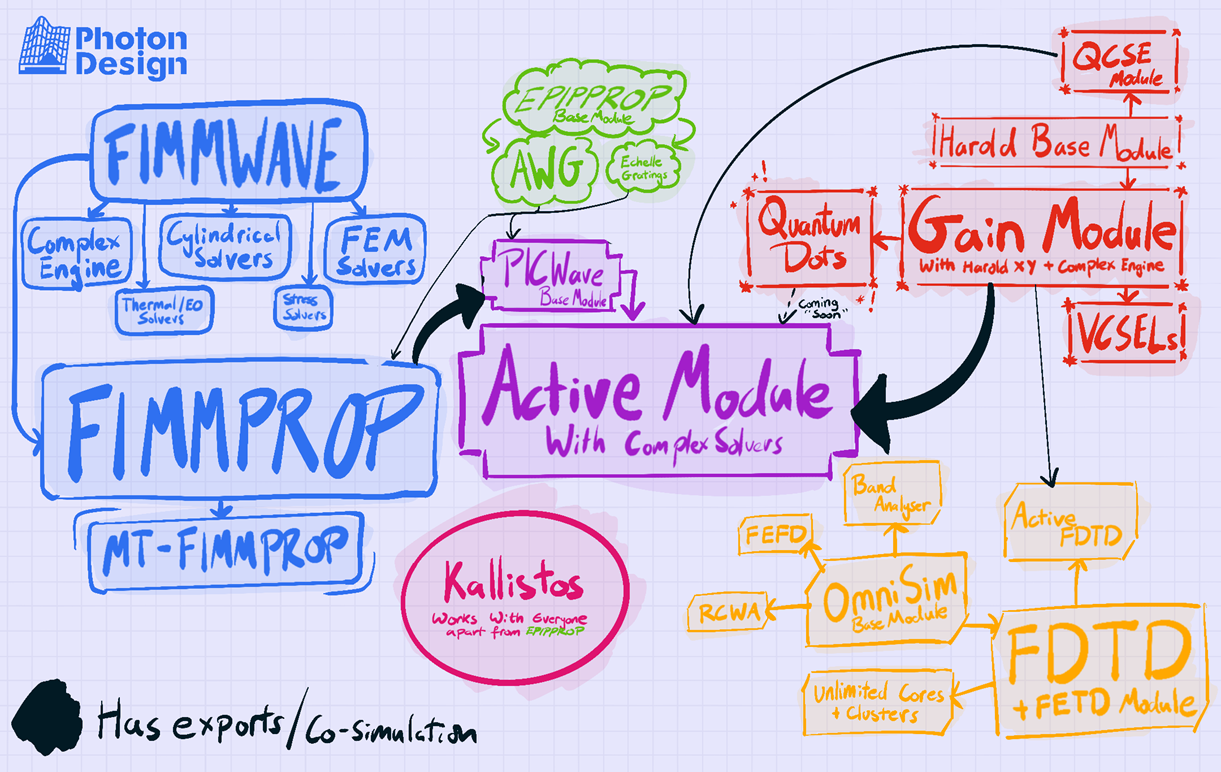
For more information on Photon Design's suite of photonic CAD tools, visit our pages on FIMMWAVE , MT-FIMMPROP , and PICWAVE .
Master FIMMPROP with our video library
Discover the power of FIMMPROP with our video guides. Whether you’re new or experienced, our videos will help you unlock the full potential of FIMMPROP features and capabilities.
