Blog
Classic Physical Optics
FRED uses “Gaussian Beam Decomposition” for propagating coherent fields through optomechanical systems. This very fast and efficient method can be used to accurately model a wide variety of physical optics.
“Gaussian Beam Decomposition” involves three steps:
The above steps happen transparently to the user and phenomena such as diffraction and interference are included inherently in the algorithm, thus making it a flexible and easy-to-use technique.
This article demonstrates using FRED to model some classic, well-known cases.
Fraunhofer Diffraction
The model to calculate the Fraunhofer diffraction is very simple and requires only a source with the desired aperture shape, and an Analysis Surface located in the Far Field.
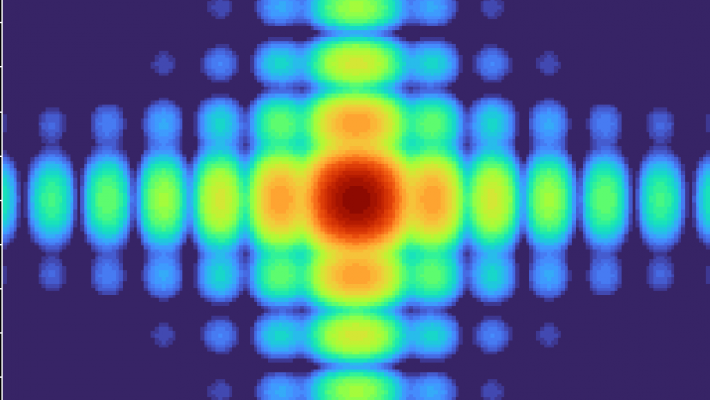
The Airy pattern and the two-dimensional Sinc2 Fraunhofer diffraction pattern of a circular and square aperture respectively are shown in the images below.

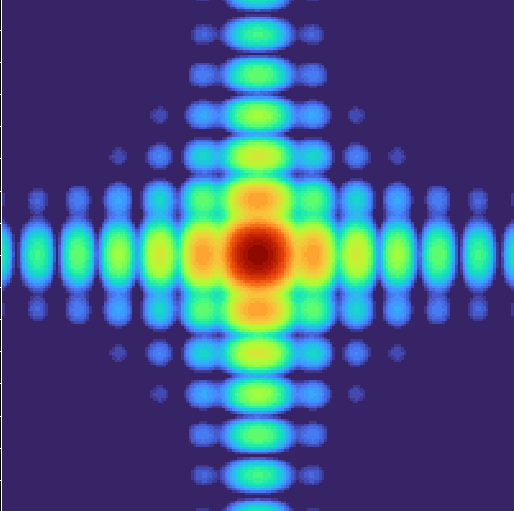
These patterns were calculated using a source with 20mm semi-aperture at a wavelength of 500nm, with an Analysis Surface 2.5km away.
Fresnel Diffraction
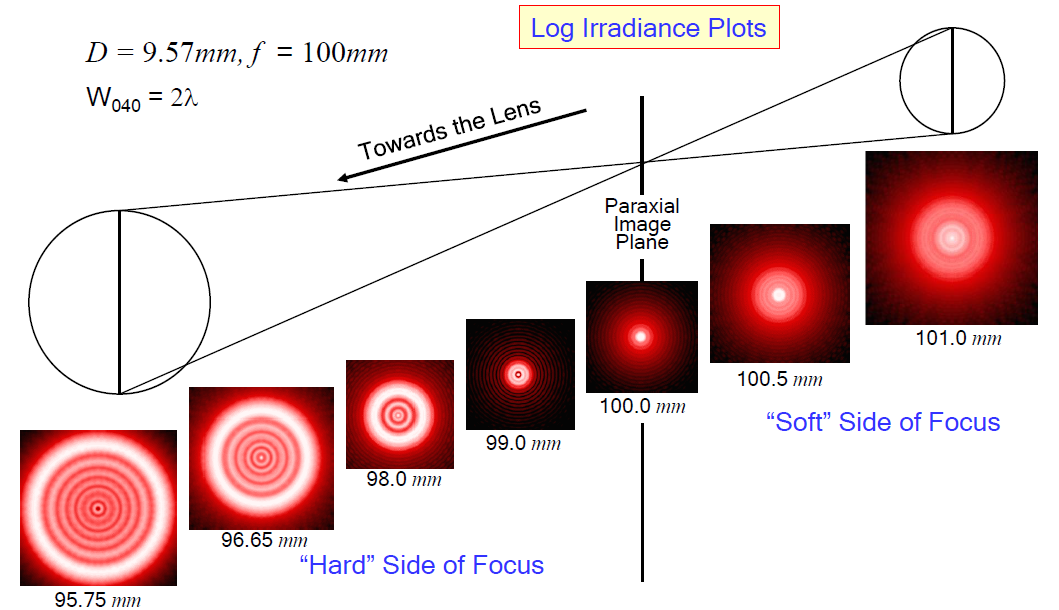
Fresnel diffraction patterns are defocused Fraunhofer diffraction patterns. The image below shows the point spread functions (PSFs) either side of focus of an unaberrated imaging system with a circular aperture.
This series of calculations was automated by using FRED’s built-in scripting capability to move the Analysis Surface in increments and calculating the Irradiance. The Fresnel diffraction patterns are defocused Airy patterns.
Spot of Arago (Poisson’s Spot)
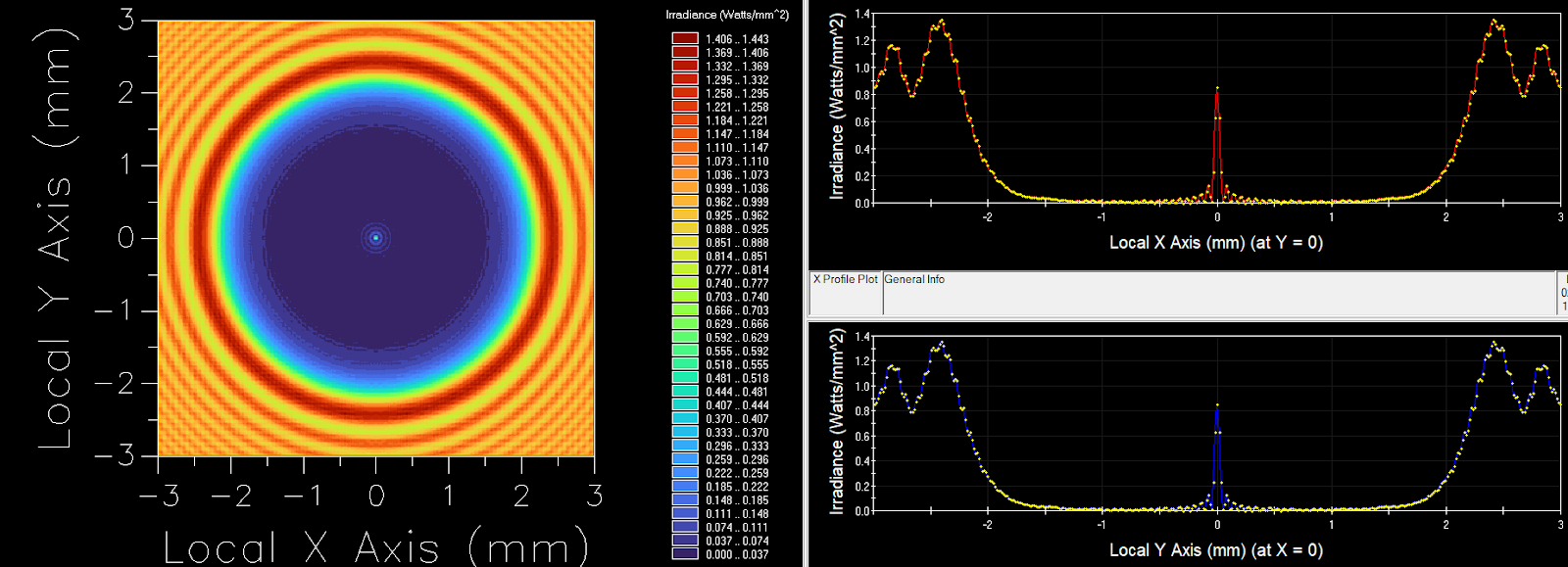
In FRED, a 2 mm diameter circular obscuration is placed in front of a 0.6328um source of 8 mm diameter circular aperture.
Placing an Analysis Surface at a distance of 400 mm from the aperture, we can observe the Spot of Arago at the center of the obscuration’s shadow.
Young’s Slits
Young's slits can be modeled very simply by placing two coherent point sources of the same wavelength at the location of each aperture.
The following image is for a wavelength of 0.5um, for two slits separated by 0.5mm, with the distance to the observation plane 1000mm. We can calculate the stationary sinusoidal interference fringe pattern.

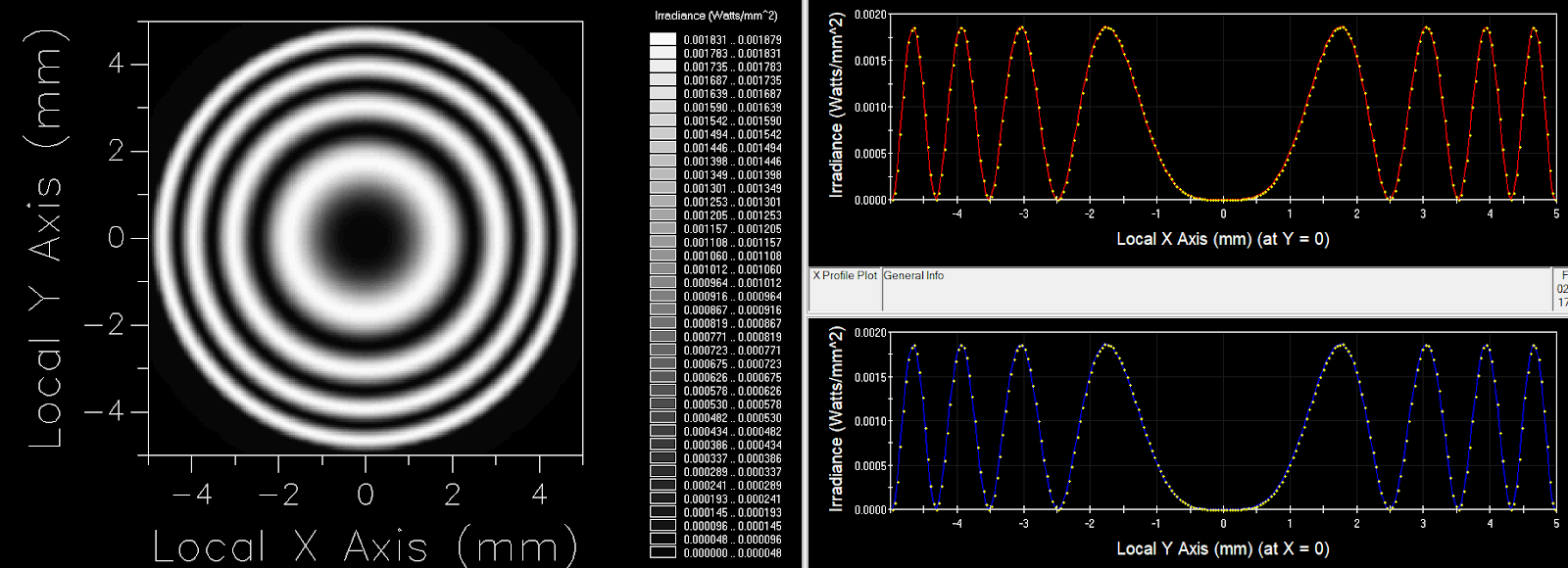
Newton’s Rings
Newton’s rings are observed when a long-radius spherical optical surface is placed on an optically flat test plate creating an interference pattern and the irradiance profile across the center of the pattern.
The center of the interference pattern is dark rather than bright because reflection from glass/air interface has a pi/2 phase change associated with it but the reflection from the subsequent air/glass interface does not.
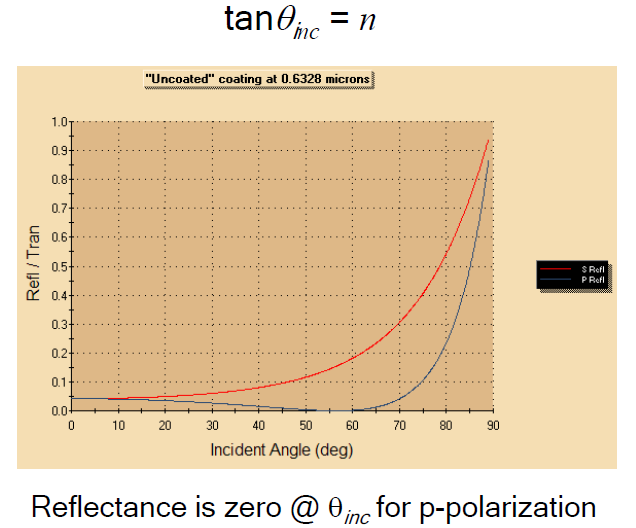
Brewster’s Angle
Brewster’s angle is the unique incident angle for which the reflected beam is completely linearly polarized. The image below shows the reflection for both s and p polarizations from a planar air/N-BK7 surface. Notice that there is no p-polarized component for light (0.6328um wavelength) when incident at around 56.5 degrees.
Summary
FRED’s Gaussian Beam Decomposition is a flexible method to model a variety of physical optics phenomena. Further examples could include Babinet’s principle, Talbot effect, frustrated total internal reflection, speckle, pulse propagation, optical fiber coupling efficiency, white light interferometry, Maltese cross, partial coherence, among others.
Contact us to request a Demo of FRED or talk through your application needs in more detail.