Blog
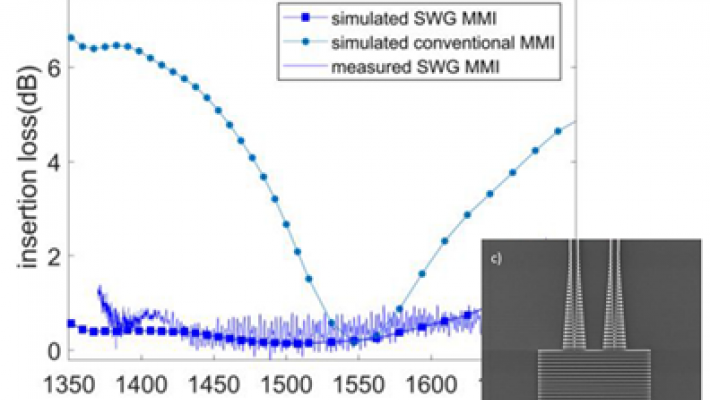
Exploring the Use of Photon Design in Photonic Innovations
How is Photon Design Being Used?
Photon Design's powerful simulation tools continue to support

Precise Light Source and Material Measurement with the Gonio'2pi Gonioradiometer
The gonio'2pi Gonioradiometer, developed by our esteemed partner opsira, offers a professional a

Celebrating the First Anniversary of the JWST's Stunning Color Photo Release
One year ago, the world witnessed a groundbreaking moment in space exploration as the James Webb Spa
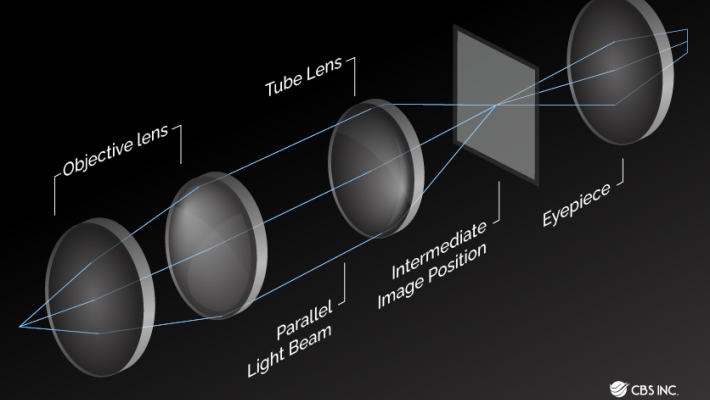
Infinity in Optics
Infinite Curvature
Infinity comes up often in optics when talking about the curvature of surfaces

How to Choose The Right Detector?
When using optical measurement systems such as an integrating sphere or a goniophotometer, it's impo

What are Diffusers?
Optical Diffusers are used to evenly distribute light, typically creating a lambertian emission prof

Integrating Spheres
Fundamentals
Integrating spheres collect electromagnetic radiation from a source and are typicall

Goniophotometer
A goniophotometer, as defined by CIE70-1987 is "a photometer for the measurement of the angular depe

Goniophotometry
Goniophotometry is a method of measuring the angular distribution of ambient light or light scattere
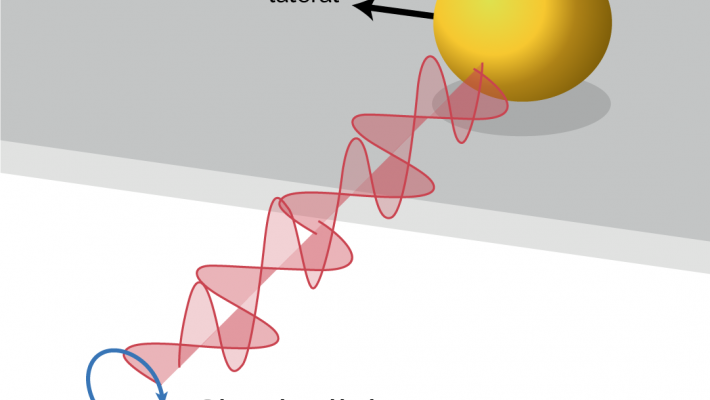
May The “Optical Force” Be With You
What is the "optical force"?
"Optical force" is a phenomenon whereby beams of light can attract and
