Blog

FIMMWAVE 8.1.0 Release: MT-FIMMPROP Updates
CBS Inc. is thrilled to announce the latest release of FIMMWAVE 8.1.0 from Photon Design, featuring
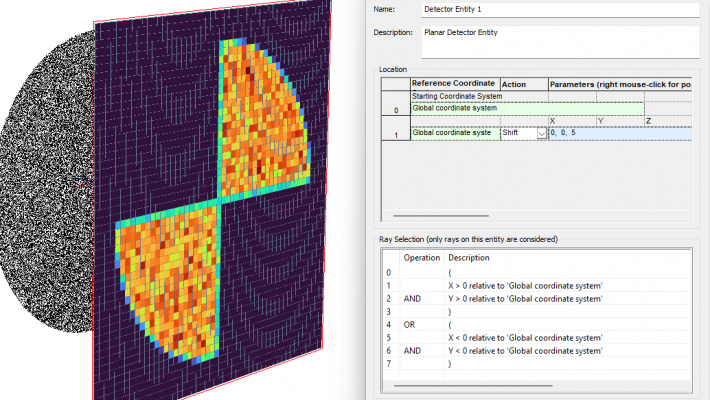
FRED Version 24.10 Release
CBS Inc. is excited to announce the latest FRED Optical Engineering Software Release, packed with ne
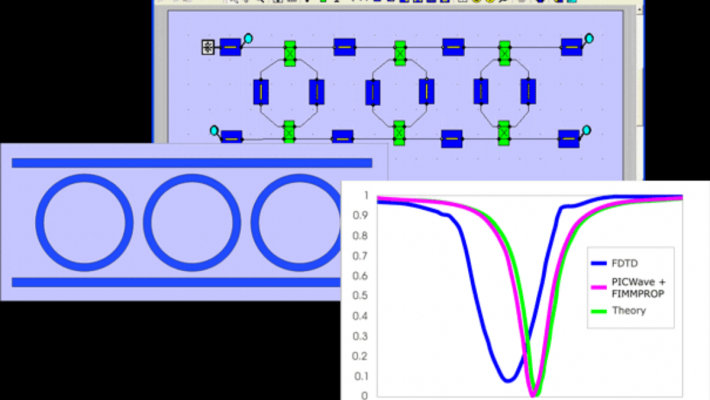
PICWave 6.2.0 Release: What's New
CBS Inc. is thrilled to announce the latest release of PICWave 6.2.0 from Photon Design, bringing ne

FRED Development Release v.24.10
Introducing FRED Development Release v.24.10!
The latest development release of FRED, v.24.10, is

OmniSim v8.1 Release
This new release of OmniSim includes the following improvements to the FDTD (Finite Difference Time
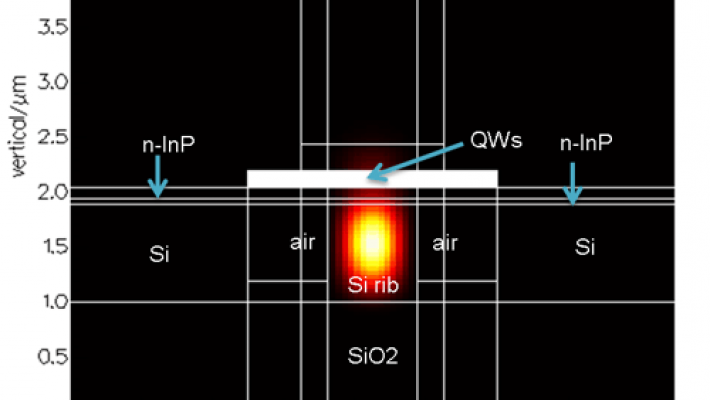
HAROLD Version 7.1 Release
HAROLD version 7.1 new feature highlights
Harold, HaroldXY and HaroldVCSEL modules: added wurtzite
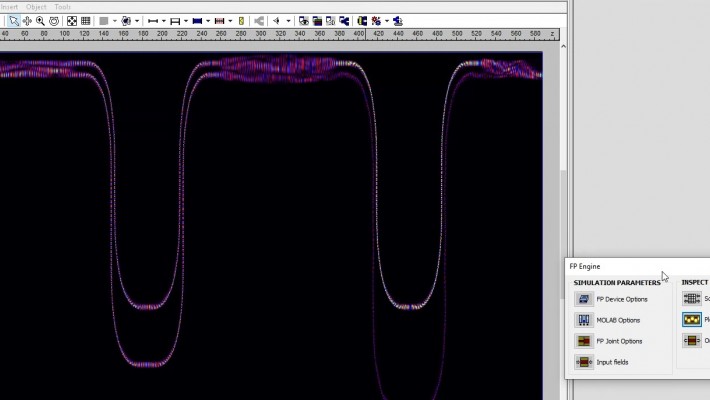
MT-FIMMPROP - Revolutionizing Optical Circuit Simulation
MT-FIMMPROP has been added as a new optional feature for FIMMWAVE.
MT-FIMMPROP is a flexible layout
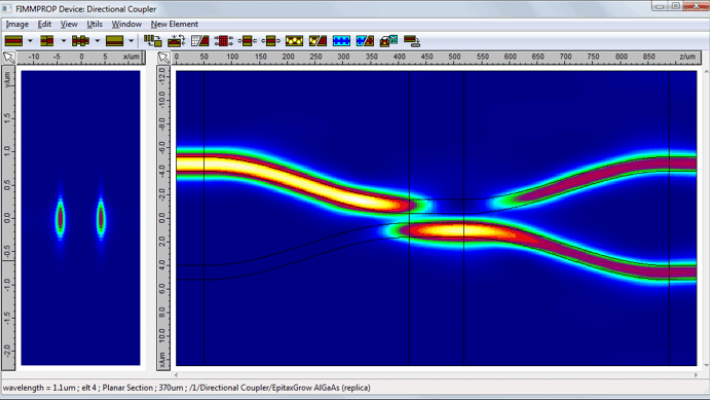
FIMMWAVE Version 8.0 Release
FIMMWAVE v8.0
Network and remote access license features have been extended to allow remote connect
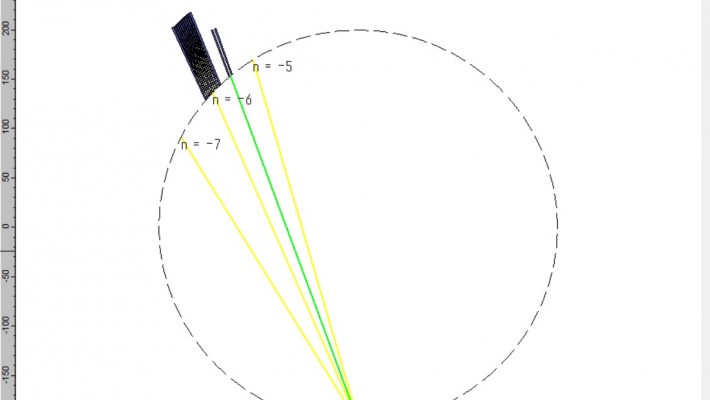
Release of EPIPPROP Version 3.4
Real-world design of AWGs and Echelle gratings with EPIPPROP version 3.4
This new version of EPIPPR
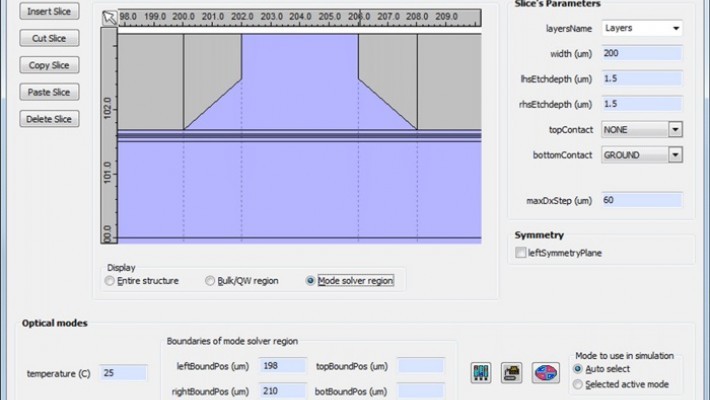
HAROLD Version 7.0: Introducing "k.p." Model to Enhance Quantum Well Simulation
HAROLD version 7.0 now has a k.p. model for improved simulation of quantum wells.
The new version o
